{tidydice} 1.0.0 is here!

Why {tidydice}

A basic understanding of probability and statistics is crucial for data understanding. A great way to teach probability and statistics is to start with an experiment, like rolling a dice or flipping a coin.

{tidydice} simulates rolling a dice and flipping a coin. Each experiment generates tidy data (tibble). Dice rolls and coin flips are simulated using sample(). The properties of the dice can be changed, like the number of sides. A coin flip is simulated using a two sided dice. Experiments can be combined with the pipe-operator.

Design

The default dice design is black/white with gold as highlight for a success. To make it reproducible, use seed

# use package
library(tidydice)
  
# example: roll dice 6 times
roll_dice(times = 6, seed = 123) |>
  plot_dice()

You can control the design of dice using plot_dice() arguments:

• fill = fill color of dice
• fill_success = fill color of dice if result is a success
• point_color = color of points
• line_color = color of lines
• line_size = size of lines

roll_dice(times = 6, seed = 123) |> 
  plot_dice(fill = "darkgrey", 
            fill_success = "darkblue",
            line_color = "white",
            point_color = "white")

Repeat

We see 2 six. This is more than th expected value, which is 1. (A dice has 6 sides, so the probability of getting a six is 1/6)

Now let’s repeat this experiment 6 times

roll_dice(times = 6, rounds = 6, seed = 123) |> 
  plot_dice(fill = "darkgrey", 
            fill_success = "darkblue",
            line_color = "white",
            point_color = "white")

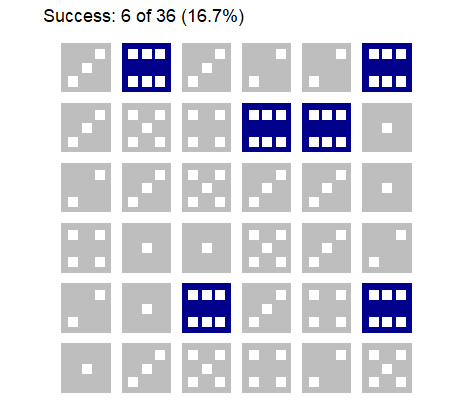
Now we get 6 six. This is excactly the expected value.

Aggregate

Lets increase rounds to 10 000. To see how many times we got a six in each round, use agg = TRUE

roll_dice(times = 6, rounds = 10000, agg = TRUE, seed = 123)

# A tibble: 10,000 × 4
   experiment round times success
        <int> <int> <int>   <int>
 1          1     1     6       2
 2          1     2     6       2
 3          1     3     6       0
 4          1     4     6       0
 5          1     5     6       2
 6          1     6     6       0
 7          1     7     6       0
 8          1     8     6       1
 9          1     9     6       0
10          1    10     6       1
# … with 9,990 more rows

We get a tibble, where each row represents one round.

Let’s use {explore} to visualise the result

roll_dice(times = 6, rounds = 10000, agg = TRUE, seed = 123) |>
  explore(success)

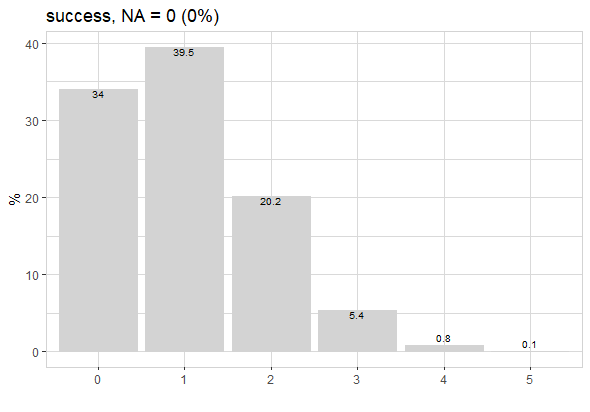
Binomial Distribution

By repeating the experiment 10 000 times we already get pretty close to the Binomial Distribution:

binom_dice(times = 6)

# A tibble: 7 × 3
  success         p      pct
    <int>     <dbl>    <dbl>
1       0 0.335     33.5    
2       1 0.402     40.2    
3       2 0.201     20.1    
4       3 0.0536     5.36   
5       4 0.00804    0.804  
6       5 0.000643   0.0643 
7       6 0.0000214  0.00214

binom_dice(times = 6) |>
  plot_binom(highlight = 3:6)

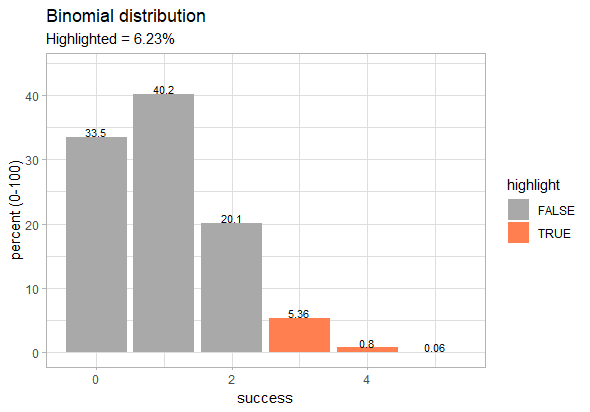
The chance to get 3 or more six is just 6.23%

Cheating

We can cheat by increasing the probability of getting a six from 1/6 (0.167) to 1/2 (0.5).

roll_dice(
  times = 6, 
  prob = c(0.1,0.1,0.1,0.1,0.1,0.5), 
  seed = 123
) |> plot_dice()

Can this cheating be detected? 3 six is still in a normal range.

Let’s do an experiment!

roll_dice(times = 6, rounds = 10000, agg = TRUE) |>
  roll_dice(
    times = 6, rounds = 10000, agg = TRUE, 
    prob = c(0.1,0.1,0.1,0.1,0.1,0.5)) |> 
  explore(success, target = experiment)

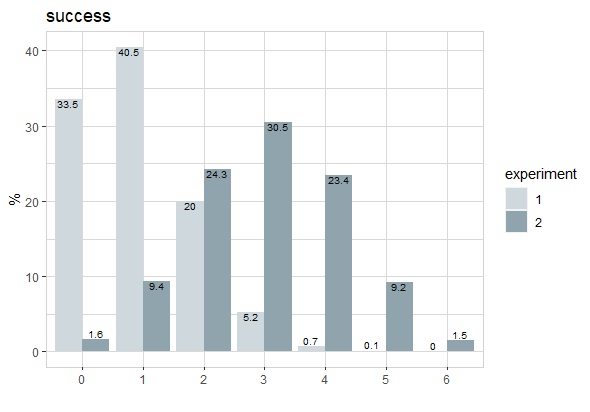
The plot shows, that there is a high chance that the cheating will be detected, if we roll the dice multiple times. Because getting 4 or more six is very unlikely if there is no cheating.

Using Dice Formula

If you want to do more complex dice rolls, use roll_dice_formula() (many thanks to Giovanni Marco for contributing the code!)

roll_dice_formula(
  dice_formula = "4d6", # 4 dice with 6 sides
  success = 15:24,      # success: sum between 15 and 24
  seed = 123            # random seed to make it reproducible
)

# A tibble: 1 × 7
  experiment dice_formula label round    nr result success
       <int> <chr>        <chr> <int> <int>  <dbl> <lgl>  
1          1 4d6          4d6       1     1     18 TRUE  

# 4 dice with 6 sides + 1 dice with 10 sides
# repeat 1000 times
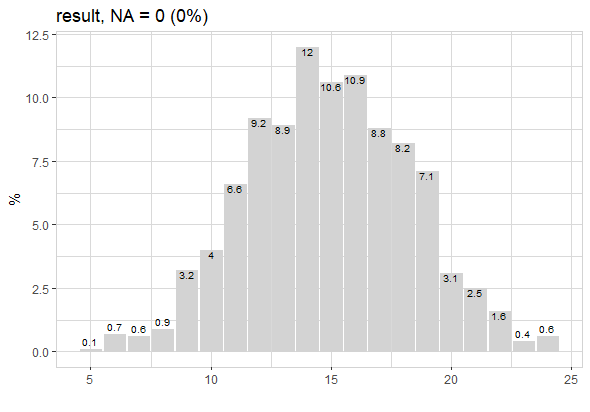
roll_dice_formula(
  dice_formula = "4d6+1d10", 
  rounds = 1000) |> 
  explore_bar(result, numeric = TRUE)

Other examples for dice_formula:

• 1d6 = roll one 6-sided dice
• 1d8 = roll one 8-sided dice
• 1d12 = roll one 12-sided dice
• 2d6 = roll two 6-sided dice
• 1d6e6 = roll one 6-sided dice, explode dice on a 6
• 3d6kh2 = roll three 6-sided dice, keep highest 2 rolls
• 3d6kl2 = roll three 6-sided dice, keep lowest 2 rolls
• 4d6kh3e6 = roll four 6-sided dice, keep highest 3 rolls, but explode on a 6
• 1d20+4 = roll one 20-sided dice, and add 4
• 1d4+1d6 = roll one 4-sided dice and one 6-sided dice, and sum the results

Weblinks

• {tidydice} on Github: https://github.com/rolkra/tidydice
• {explore} on Github: https://github.com/rolkra/explore